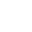How To Install OpenJDK 17 On Mac
It provides all the steps required to install OpenJDK 17 on Mac systems including macOS Sierra, High Sierra, Mojave, Catalina, and Big Sur.
This tutorial provides all the steps required to install the open source version of Java i.e. OpenJDK 17 on Mac systems. It provides the steps required to install OpenJDK 17 on macOS Catalina. The steps should be the same for other versions of macOS including Sierra, High Sierra, Mojave, and Big Sur.
Notes: As an alternative to the commercial releases of Java i.e. Oracle Java, we can use OpenJDK for personal, development, and commercial usage without purchasing any license. Also, OpenJDK is distributed by Oracle under the GNU General Public License, version 2, with the Classpath Exception, and available on http://jdk.java.net.
System Checks
In this step, we will test whether Java is already installed or not. To do so, open the terminal and type java -version as shown in Fig 1. It shows that Java is already installed on my system.

Fig 1
It might show the message - "No Java runtime present, requesting install" in absence of Java and also opens a dialog to know more about it as shown in Fig 2.
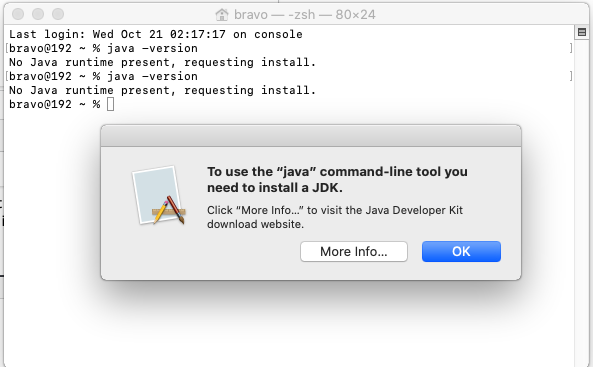
Fig 2
Click the OK Button to hide the dialog in case it's displayed on your system in absence of Java.
Download OpenJDK 17
Open the download link to select the available versions as shown in Fig 3.
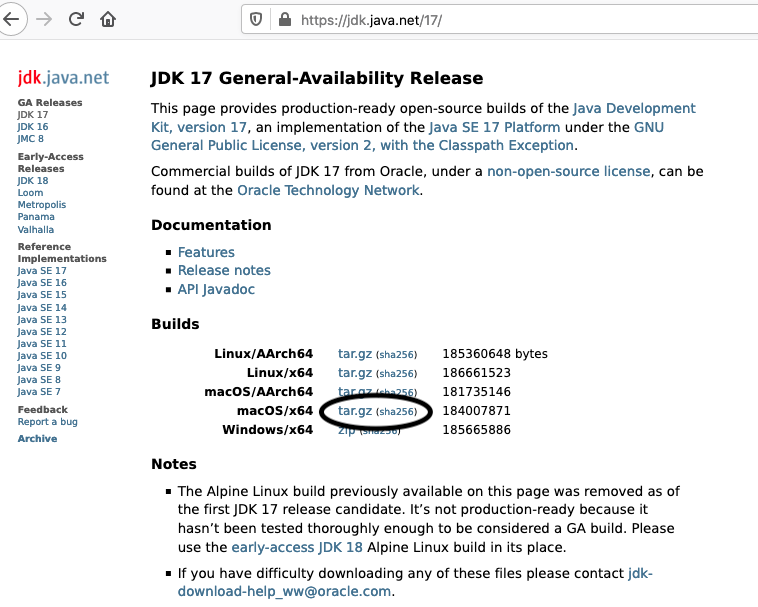
Fig 3
Click the Download Link as highlighted in Fig 3 to download OpenJDK 17 for macOS.
Install JDK
The default location used by macOS to search for the available JDK is - /Library/Java/JavaVirtualMachines. We can use the below-mentioned command to find the available JDKs installed on the system.
# List installed JDKs
/usr/libexec/java_home -V
It will list down the available JDKs as shown in Fig 4.
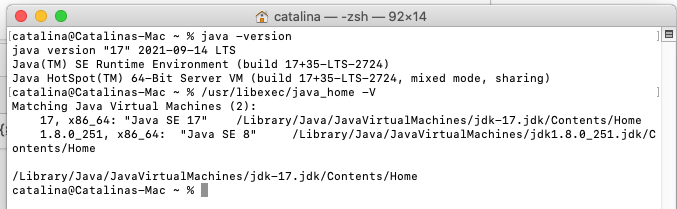
Fig 4
Now, install the OpenJDK downloaded in the previous step using the commands as shown below.
# Move to the download location
cd ~/Downloads
# Check the downloaded file name using ls -la command
# Extract the download
tar -xf openjdk-17_macos-x64_bin.tar.gz
# Check the OpenJDK version using the list command
# Output of ls -la command on my system
total 722256
drwx------@ 7 catalina staff 224 Sep 26 07:05 .
drwxr-xr-x+ 17 catalina staff 544 Sep 26 06:14 ..
-rw-r--r--@ 1 catalina staff 6148 Sep 26 06:16 .DS_Store
-rw-r--r-- 1 catalina staff 0 Apr 18 2020 .localized
drwxr-xr-x@ 3 catalina staff 96 Aug 5 18:27 jdk-17.jdk
-rw-r--r--@ 1 catalina staff 176826806 Sep 26 06:24 jdk-17_macos-x64_bin.dmg
-rw-r--r--@ 1 catalina staff 184007871 Sep 26 07:03 openjdk-17_macos-x64_bin.tar.gz
Optionally, remove the existing Oracle JDK 17. I have removed the existing Oracle JDK 17 (Fig 1 and Fig 4) to install OpenJDK 17. You may also rename the OpenJDK 17 to install it parallel to the existing Oracle JDK 17.
# Uninstall existing Oracle JDK 17
sudo rm -rf "/Library/Java/JavaVirtualMachines/jdk-17.jdk"
Install OpenJDK 17 extracted by us.
# Install the JDK
sudo mv jdk-17.jdk /Library/Java/JavaVirtualMachines/
Now we will verify the installation as shown below.
# Check Java version
java -version
# It should show the version installed by us
openjdk version "17" 2021-09-14
OpenJDK Runtime Environment (build 17+35-2724)
OpenJDK 64-Bit Server VM (build 17+35-2724, mixed mode, sharing)
You might be required to switch the active JDK in case it does not reflect the OpenJDK 17. Again check the list of installed JDKs as shown below.
# List installed JDKs
/usr/libexec/java_home -V
# It will output the list of the available JDKs
Matching Java Virtual Machines (2):
17, x86_64: "OpenJDK 17" /Library/Java/JavaVirtualMachines/jdk-17.jdk/Contents/Home
1.8.0_251, x86_64: "Java SE 8" /Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home
/Library/Java/JavaVirtualMachines/jdk-17.jdk/Contents/Home
It should list the OpenJDK 17 installed by us. This is how we can install and verify Java on macOS. The installation commands used by me are shown in Fig 5.
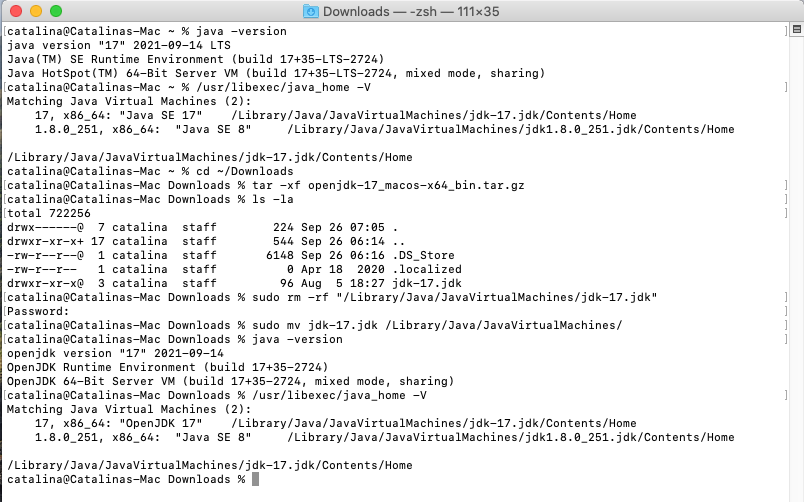
Fig 5
Switch JDK
We can switch between the multiple JDKs using the command as shown below.
# List installed JDKs
/usr/libexec/java_home -V
# Switch active JDK
export JAVA_HOME=`/usr/libexec/java_home -v <version>`
# Example
export JAVA_HOME=`/usr/libexec/java_home -v 1.8.0_251`
This switches the Java version for the active shell. If you close the terminal and again check the Java version by opening a new terminal, your changes won't be reflected. You can follow How To Switch Java Version On Mac to system-wide update the Java version.
Getting started with Java - Hello World
In this step, we will write, compile, and execute our first program in Java using the standard Hello World example.
Now write the first Java program as shown below, save the program as HelloWorld.java and exit the editor. Make sure that the class name and file name are the same.
class HelloWorld {
public static void main( String[] args ) {
System.out.println( "Hello World !!" );
}
}
Now open the command prompt and navigate to the path where you have saved your Java program. Use the below-mentioned commands to compile and execute the program.
# Compile - Specify file name and extension
javac HelloWorld.java
# Execute - Spicy file name
java HelloWorld
# Output
Hello World !!
These are the easy to install steps required to install Oracle JDK on Mac and write, compile and execute the first Java program.
Summary
This tutorial provided all the steps required to install Oracle JDK 17 on Mac and also provided the steps required to compile and run the first Java program using a simple Hello World program.